本文聚焦数学视角下的 Transformer 学习体系，将复杂的知识体系拆解为三个递进阶段：基础数学工具奠基（线性代数+概率论）、模型训练核心解析（微积分+优化理论+信息论）、结构设计与工程落地（数值分析+高阶拓展理论）。每个阶段不仅明确了需掌握的数学知识点与核心学习目标，还补充了理论与实践结合的技巧，帮助学习者从数学原理出发，逐步穿透 Transformer 的结构逻辑、训练机制与工程细节，最终实现“能看懂公式、会推导机制、可分析稳定性、懂表达边界”的进阶目标。

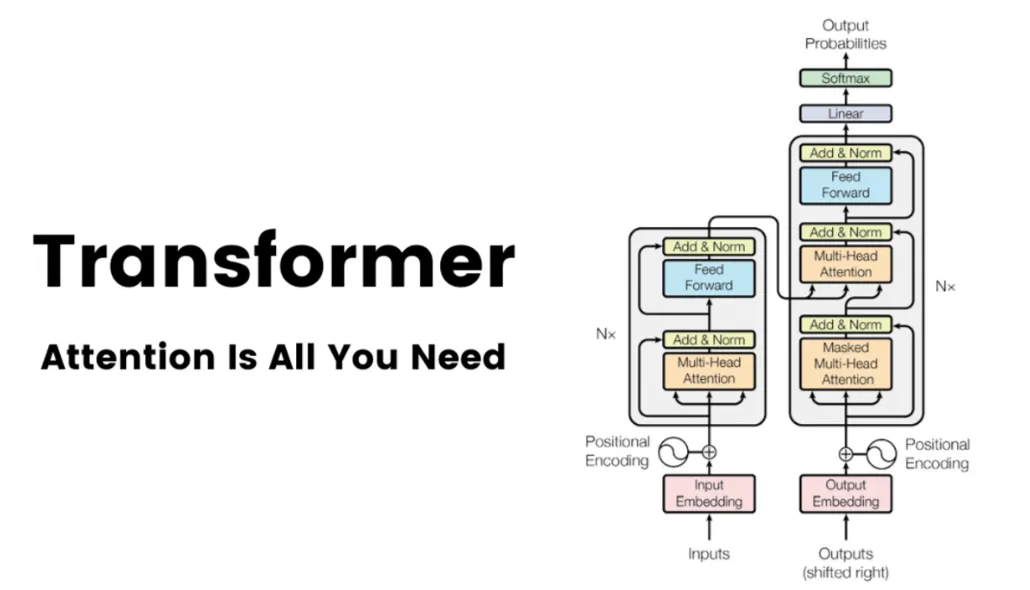
这份 「数学驱动的 Transformer 学习路线图」，并非简单罗列知识点，而是以“数学原理→模型应用”为核心逻辑，按基础奠基 → 核心突破 → 拓展深化的阶段划分，让你避开“只知模型结构、不懂数学本质”的学习误区，真正从底层理解 Transformer 为何能成为深度学习的核心架构。

一、 核心梳理：Transformer 依赖的数学领域及其作用

Transformer 的每个关键模块，背后都对应着特定的数学理论支撑。下表清晰拆解了各数学领域在模型中的具体应用场景：

数学领域	在 Transformer 中的核心作用	关联模型模块举例
线性代数	构建数据表示与核心计算逻辑，是模型的“骨架”	词向量表示、注意力分数计算、矩阵乘法操作
概率论	解释模型输出逻辑，量化预测不确定性	softmax 概率分布、交叉熵损失、语言建模任务
优化理论	驱动模型迭代更新，解决“如何高效学习”的问题	SGD/Adam 优化器、学习率调整、收敛性保障
微积分	提供梯度计算的数学基础，是反向传播的“引擎”	链式法则求导、梯度下降方向计算、自动微分
信息论	解释注意力的“信息筛选”机制，优化损失函数设计	交叉熵的信息意义、KL 散度、注意力的信息聚焦
组合数学	支撑模型结构设计，解决“如何覆盖多维度信息”的问题	多头注意力的组合逻辑、位置编码的排列规则
数值分析	保障训练过程稳定，规避数值异常导致的模型崩溃	LayerNorm 数值调节、残差连接防梯度消失

二、 分阶段学习路线：从数学基础到 Transformer 精通

学习过程需遵循“先工具、后核心、再拓展”的逻辑，避免跳跃式学习导致的基础薄弱问题。具体阶段划分如下：

第一阶段：数学基础奠基——掌握模型“语言”
第二阶段：核心训练解析——理解模型“如何学习”
第三阶段：结构与工程深化——保障模型“稳定好用”

🚩 第一阶段：数学基础奠基——构建 Transformer 的“语言体系”

此阶段的核心目标是：掌握 Transformer 中数据表示、计算逻辑与输出解释的基础数学工具，能看懂模型中最基本的公式与符号含义。

📘 1. 线性代数：模型的“计算骨架”

Transformer 中几乎所有核心操作（如注意力计算、线性变换）都依赖线性代数，需重点掌握“运算规则+几何意义”，而非单纯记忆公式。

• ✅ 向量与矩阵：词向量的表示形式、矩阵乘法的“行乘列”规则（尤其注意注意力计算中“Q×K^T”的维度匹配）
• ✅ 线性变换：矩阵如何实现向量的“缩放+旋转”（如全连接层本质是对输入向量的线性变换）
• ✅ 特征值与奇异值：理解矩阵的“主成分”（如 PCA 降维的数学原理，可辅助理解词向量降维可视化）
• ✅ 张量：高阶矩阵的表示与运算（如 batch 维度下的“样本×序列长度×词向量维度”三阶张量）

📚 推荐资源与学习技巧：

• 书籍：《Linear Algebra Done Right》（侧重理论理解，避开繁琐计算）、《工程数学线性代数》（侧重应用场景）
• 视频：3Blue1Brown《线性代数的本质》（用动画解释线性变换、行列式等核心概念，必看）
• 技巧：学完一个知识点后，尝试对应到 Transformer 场景（如学完矩阵乘法，手动推导“Q×K^T”的维度变化）

📘 2. 概率论与统计：模型的“输出解释器”

Transformer 的输出（如文本生成的概率分布）需用概率论解释，核心是理解“如何从 logits 到概率，再到损失计算”。

• ✅ 随机变量与概率分布：离散分布（如文本 token 的类别分布）、连续分布（如模型参数的初始化分布）
• ✅ 条件概率与联合分布：理解“给定前一个 token，预测下一个 token”的条件概率逻辑（语言建模的核心）
• ✅ 最大似然估计（MLE）：模型为何要“最大化样本的对数似然”（本质是让模型预测与真实样本尽可能一致）
• ✅ 交叉熵损失：从 KL 散度推导交叉熵，理解“为何交叉熵能衡量模型预测与真实分布的差距”
• ✅ softmax 函数：数学公式推导（softmax(x_i) = e^x_i / Σe^x_j），以及它“将 logits 映射为概率分布”的作用（注意数值稳定性问题，如减去最大值防止 e^x 溢出）

📚 推荐资源与学习技巧：

• 书籍：《概率论基础》（Sheldon Ross，侧重理论）、《统计学习方法》（李航，第2章概率模型基础）
• 讲义：斯坦福 CS229 机器学习课程概率部分（结合机器学习场景，案例更贴近 Transformer）
• 技巧：手动推导交叉熵损失与 softmax 的关系，理解“为何分类任务常用交叉熵+softmax”

🚩 第二阶段：核心训练解析——让模型“活起来”

此阶段的核心目标是：理解 Transformer 如何通过“梯度计算→优化更新”实现学习，掌握训练过程中的数学原理与关键挑战。

📘 3. 微积分：模型训练的“动力引擎”

反向传播是 Transformer 训练的核心，而微积分（尤其是多变量微积分）是反向传播的数学基础。

• ✅ 导数与偏导数：单变量函数的导数（如 sigmoid 函数的导数）、多变量函数的偏导数（如损失函数对每个模型参数的偏导）
• ✅ 梯度：偏导数组成的向量，代表“损失函数下降最快的方向”（梯度下降的核心依据）
• ✅ 链式法则：多函数复合后的求导规则（反向传播的核心，需熟练掌握“从输出层到输入层”的梯度传递过程，如手动推导单隐藏层神经网络的反向传播）
• ✅ Hessian 矩阵：二阶偏导数组成的矩阵，理解“梯度下降的曲率”（可选，帮助理解优化器中动量、二阶矩估计的作用）
• ✅ 自动微分：PyTorch/TensorFlow 如何“记录计算图→自动求导”（无需深入源码，只需理解“动态图vs静态图”的求导逻辑）

📚 推荐资源与学习技巧：

• 书籍：《微积分学教程》（托马斯，侧重基础）、《深度学习中的数学》（斋藤康毅，结合深度学习场景）
• 视频：MIT OCW 18.01 单变量微积分、18.02 多变量微积分（系统讲解，案例经典）
• 技巧：用 PyTorch 的 backward() 函数实操简单模型（如线性回归），观察梯度变化，对应到微积分理论

📘 4. 优化理论：模型学习的“导航系统”

有了梯度（方向），还需通过优化理论确定“如何走”（步长、更新策略），才能让模型高效收敛。

• ✅ 凸优化 vs 非凸优化：理解 Transformer（非凸模型）与线性回归（凸模型）的优化差异（非凸模型可能陷入局部最优，需依赖初始化、学习率等策略）
• ✅ 基础优化器原理：
  • SGD：随机梯度下降（用 batch 样本估计梯度，减少计算量）
  • Momentum：模拟“物理惯性”，加速收敛（减少梯度震荡）
  • Adam：结合动量与自适应学习率（目前 Transformer 最常用的优化器，需理解一阶矩、二阶矩估计的作用）
• ✅ 学习率调整：学习率过大导致发散、过小导致收敛慢（需掌握 StepLR、CosineAnnealingLR 等调整策略）
• ✅ Loss Landscape：损失函数的“地形”（理解 Transformer 深层模型中“鞍点”“平坦区域”对优化的影响）

📚 推荐资源与学习技巧：

• 书籍：《Convex Optimization》（Boyd & Vandenberghe，前三章掌握凸优化基础）、《深度学习》（Goodfellow 等，第8章优化算法）
• 博客：Ruder 博客《An overview of gradient descent optimization algorithms》（系统对比各优化器）
• 技巧：用不同优化器（SGD、Adam）训练同一简单模型（如 MNIST 分类），观察训练 loss 曲线差异

📘 5. 信息论：模型“信息筛选”的数学依据

注意力机制的“聚焦关键信息”、损失函数的“最小化不确定性”，都可通过信息论解释，帮助理解模型设计的深层逻辑。

• ✅ 熵（Entropy）：量化“随机变量的不确定性”（如均匀分布的熵最大，说明不确定性最高；确定分布的熵为0）
• ✅ 交叉熵（Cross Entropy）：从“真实分布”与“模型预测分布”的信息差异出发，理解为何交叉熵能作为损失函数（交叉熵越小，两个分布越接近）
• ✅ KL 散度（相对熵）：量化两个分布的“距离”（交叉熵 = 熵 + KL 散度，当真实分布固定时，最小化交叉熵等价于最小化 KL 散度）
• ✅ 互信息：衡量两个随机变量的“关联程度”（可选，帮助理解注意力机制中“查询Q与键K的关联强度”）
• ✅ 信息瓶颈理论：模型如何“压缩无关信息、保留关键信息”（可选，理解 BERT 等预训练模型的信息筛选逻辑）

📚 推荐资源与学习技巧：

• 书籍：《Elements of Information Theory》（Cover & Thomas，信息论经典教材，重点看熵、交叉熵、KL 散度章节）
• 课程：吴恩达机器学习课程信息论部分（结合分类任务，案例易懂）
• 技巧：用信息论解释“为何注意力权重能反映 token 间的重要性”（权重越高，互信息越大，关联越强）

---

🚩 第三阶段：结构与工程深化——让模型“稳定且强大”

此阶段的核心目标是：理解 Transformer 结构设计（如位置编码、多头注意力）的数学逻辑，以及工程实现中（如训练稳定性）的数值保障手段。

📘 6. 数值分析：训练稳定性的“守护神”

Transformer 深层结构易出现梯度消失/爆炸、数值溢出等问题，数值分析是解决这些问题的关键。

• ✅ 浮点数精度：理解 float32/float16 等精度的数值范围（如 float16 易溢出，需用混合精度训练）
• ✅ 数值误差传播：梯度在反向传播中如何因“多次乘法”导致消失（如 sigmoid 导数小于0.25，深层后梯度趋近于0）或爆炸（如权重初始化过大，梯度累积）
• ✅ 激活函数的数值性质：ReLU 为何能缓解梯度消失（导数为1或0，避免梯度衰减）、GELU 为何更适合 Transformer（平滑的非线性，数值更稳定）
• ✅ LayerNorm 与 BatchNorm：理解 LayerNorm“按样本层归一化”的数学公式（(x - μ) / √(σ² + ε)），以及它“稳定层输出分布、加速收敛”的作用（对比 BatchNorm，理解为何 Transformer 更适合 LayerNorm）
• ✅ 残差连接：数学上如何“跳过层变换，直接传递梯度”（output = x + F(x)），从数值上缓解梯度消失（梯度可通过残差路径直接回传）

📚 推荐资源与学习技巧：

• 书籍：《Numerical Linear Algebra》（Trefethen，侧重数值计算的稳定性）
• 论文：Transformer 原始论文附录（详细说明训练技巧的数值依据）、《Layer Normalization》论文
• 技巧：用 PyTorch 对比“有无残差连接/LayerNorm”的模型训练效果，观察梯度变化

---

📘 7. 高阶拓展：结构设计的“数学逻辑”

此阶段需结合组合数学、图论等思想，理解 Transformer 结构创新的底层逻辑，甚至能启发新的模型设计。

• ✅ 位置编码的数学本质：正弦/余弦位置编码（PE(pos, 2i) = sin(pos/10000^(2i/d_model))）如何通过傅里叶变换表示位置信息（不同频率的正弦波对应不同的位置周期）
• ✅ 多头注意力的组合思想：为何“多个单头注意力拼接”能提升模型表达能力（从组合数学角度，每个头关注不同的信息维度，拼接后实现“多维度信息覆盖”）
• ✅ 自注意力的复杂度分析：从排列组合角度，理解自注意力 O(n²d) 的时间复杂度（n 为序列长度，每个 token 需与其他 n-1 个 token 计算注意力，共 n² 次操作）
• ✅ 图模型与 Transformer 的关联：Graph Attention Networks（GAT）如何将“节点间的注意力”与图结构结合（从图论角度，Transformer 可视为一种特殊的图模型，token 为节点，注意力为边权重）
• ✅ 稀疏注意力的数学优化：如何通过“限制注意力计算范围”（如局部注意力、滑动窗口注意力）将复杂度降至 O(nd)（可选，理解 Longformer、Performer 等模型的优化逻辑）

📚 推荐资源与学习技巧：

• 论文：《Attention Is All You Need》（原始论文，重点分析结构设计）、《Graph Attention Networks》（GAT 论文）
• 书籍：《动手学深度学习》（李沐，第16章 Transformer 部分，结合代码解析结构）
• 技巧：尝试修改 Transformer 结构（如自定义位置编码、调整多头注意力头数），观察模型性能变化，理解结构与性能的关联

---

三、 可视化学习路径：从“工具”到“精通”的逻辑链

第一阶段：掌握模型“语言”——能看懂公式
├── 线性代数 ← 搞定“数据表示与计算”（如词向量、矩阵乘法）
└── 概率论   ← 搞定“输出解释与损失”（如softmax、交叉熵）

第二阶段：理解模型“学习”——能推导机制
├── 微积分   ← 搞定“梯度计算”（反向传播、链式法则）
├── 优化理论 ← 搞定“参数更新”（优化器、学习率）
└── 信息论   ← 搞定“信息筛选”（注意力、损失的信息意义）

第三阶段：保障模型“稳定”——能分析与优化
├── 数值分析 ← 搞定“训练稳定性”（LayerNorm、残差连接）
└── 高阶理论 ← 搞定“结构创新”（位置编码、稀疏注意力）

四、 实践补充：数学理论落地的“最佳途径”

只学理论易陷入“纸上谈兵”，用代码实现简化版 Transformer，是融合数学与工程的最佳方式——通过代码，你能直观感受到“数学公式如何转化为可执行的计算”。

• ✅ 入门级实践：用 PyTorch 实现“单头自注意力”，手动计算 Q、K、V 的矩阵乘法，观察注意力权重的生成过程（对应线性代数知识）。
• ✅ 进阶级实践：实现“带残差连接与 LayerNorm 的 Transformer 编码器层”，对比“有无残差/LayerNorm”的梯度变化（对应数值分析知识）。
• ✅ 推荐资源：
  • Jay Alammar 的《The Illustrated Transformer》（用动画+代码片段解释 Transformer 结构，入门友好）
  • 《The Annotated Transformer》（PyTorch 注释版 Transformer 实现，每一行代码都对应理论解释）
  • Hugging Face Transformers 库源码（查看真实工业界模型的数学实现，如位置编码、多头注意力的代码逻辑）

---

五、 最终目标：数学视角下的 Transformer 能力图谱

通过三个阶段的学习，你将逐步构建起“从理论到实践”的完整能力体系，具体目标如下表所示：

学习阶段	核心能力目标	典型应用场景
基础阶段	1. 看懂 Transformer 中的所有数学公式 2. 解释核心模块（如注意力、softmax）的数学逻辑	阅读 Transformer 相关论文时，能理解公式含义；向他人讲解“注意力机制为何用矩阵乘法计算”
进阶阶段	1. 独立推导反向传播的梯度计算过程（如从损失函数推导至注意力层参数的梯度） 2. 基于优化理论分析“为何 Adam 比 SGD 更适合 Transformer 训练” 3. 用信息论解释交叉熵损失的设计合理性	复现论文中的模型训练流程时，能自主调整优化器参数；针对训练发散问题，从梯度计算角度定位原因
拓展阶段	1. 从数值分析角度优化模型结构（如设计更稳定的归一化层、缓解长序列梯度消失） 2. 结合组合数学与图论，提出轻量化注意力结构（如稀疏注意力、动态注意力） 3. 分析 Transformer 表达能力边界（如为何难以处理超长期依赖，需引入记忆机制）	参与模型改进项目，优化大模型训练效率；撰写技术报告，论证新结构的数学合理性；在学术讨论中，针对“Transformer 局限性”提出有理论依据的观点

六、 学习建议：避免数学与工程脱节的关键技巧

在整个学习过程中，最容易陷入“学了数学不会用”的误区。以下三个技巧能帮你打通“理论→实践”的闭环：

1. “公式→代码”映射练习：每学一个数学公式，就用代码实现一次。例如，学完自注意力公式 Attention(Q,K,V) = softmax(QK^T/√d_k)V 后，用 NumPy 手动计算 Q、K、V 的矩阵乘法，再调用 softmax 函数，观察输出结果与公式推导的一致性——这种“手动复现”能让你直观感受到“抽象公式如何转化为具体计算”。

2. “问题→数学归因”分析：遇到模型训练问题时，尝试用数学理论定位原因。比如训练时出现 loss 骤升，不要只调整学习率，先思考：是 softmax 计算时出现数值溢出（概率论数值稳定性问题）？还是梯度反向传播时出现爆炸（微积分+数值分析问题）？通过“问题归因→理论对应→解决方案”的逻辑链，强化数学与工程的关联。

3. “论文→公式拆解”复盘：阅读顶会论文（如《Attention Is All You Need》《FlashAttention》）时，重点拆解“新结构背后的数学创新”。例如，FlashAttention 用“分块计算”优化注意力，核心是基于数值分析中“减少内存访问次数以降低计算延迟”的原理；将这类创新点与已学数学知识对应，能帮你建立“从理论到创新”的思维模式。

七、 总结：数学是理解 Transformer 的“底层钥匙”

Transformer 并非“黑箱模型”，其每一个结构设计、每一步训练流程，都有严谨的数学支撑——线性代数构建了它的计算框架，概率论定义了它的输出逻辑，微积分与优化理论赋予了它学习能力，数值分析保障了它的训练稳定。

这份学习路线图的核心，不是让你成为数学专家，而是让你掌握“用数学视角拆解模型”的能力：当你能从线性代数角度看懂注意力计算，从优化理论角度调整训练策略，从数值分析角度解决工程问题时，才算真正“精通”Transformer——不仅知其然，更知其所以然，甚至能基于数学原理提出新的模型改进思路。

建议根据自身基础，按“基础阶段1-2个月→进阶阶段2-3个月→拓展阶段3-4个月”的节奏推进，每完成一个阶段，通过“代码实践+论文复盘”验证学习效果，逐步构建起系统化的知识体系。

那么，如何系统的去学习大模型LLM？

作为一名从业五年的资深大模型算法工程师，我经常会收到一些评论和私信，我是小白，学习大模型该从哪里入手呢？我自学没有方向怎么办？这个地方我不会啊。如果你也有类似的经历，一定要继续看下去！这些问题啊，也不是三言两语啊就能讲明白的。

所以我综合了大模型的所有知识点，给大家带来一套全网最全最细的大模型零基础教程。在做这套教程之前呢，我就曾放空大脑，以一个大模型小白的角度去重新解析它，采用基础知识和实战项目相结合的教学方式，历时3个月，终于完成了这样的课程，让你真正体会到什么是每一秒都在疯狂输出知识点。

由于篇幅有限，⚡️ 朋友们如果有需要全套 《2025全新制作的大模型全套资料》，扫码获取~

为什么要学习大模型？

我国在A大模型领域面临人才短缺,数量与质量均落后于发达国家。2023年，人才缺口已超百万，凸显培养不足。随着AI技术飞速发展，预计到2025年,这一缺口将急剧扩大至400万,严重制约我国AI产业的创新步伐。加强人才培养,优化教育体系,国际合作并进是破解困局、推动AI发展的关键。

👉大模型学习指南+路线汇总👈

我们这套大模型资料呢，会从基础篇、进阶篇和项目实战篇等三大方面来讲解。

👉①.基础篇👈

基础篇里面包括了Python快速入门、AI开发环境搭建及提示词工程，带你学习大模型核心原理、prompt使用技巧、Transformer架构和预训练、SFT、RLHF等一些基础概念，用最易懂的方式带你入门大模型。

👉②.进阶篇👈

接下来是进阶篇，你将掌握RAG、Agent、Langchain、大模型微调和私有化部署，学习如何构建外挂知识库并和自己的企业相结合，学习如何使用langchain框架提高开发效率和代码质量、学习如何选择合适的基座模型并进行数据集的收集预处理以及具体的模型微调等等。

👉③.实战篇👈

实战篇会手把手带着大家练习企业级的落地项目（已脱敏），比如RAG医疗问答系统、Agent智能电商客服系统、数字人项目实战、教育行业智能助教等等，从而帮助大家更好的应对大模型时代的挑战。

👉④.福利篇👈

最后呢，会给大家一个小福利，课程视频中的所有素材，有搭建AI开发环境资料包，还有学习计划表，几十上百G素材、电子书和课件等等，只要你能想到的素材，我这里几乎都有。我已经全部上传到CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

相信我，这套大模型系统教程将会是全网最齐全 最易懂的小白专用课！！