Note

• 相关讨论：SFT为啥比RL更容易导致遗忘
  • RL的本质就是一个sampling based 的优化过程，我们有一个分布，采样得到的轨迹有的reward大，有的reward小，那么我们就增大采reward大的轨迹的概率，减小采reward小的轨迹的概率。这个过程中我们希望模型更新要足够稳健，不能过于激进。
  • 打个比方，比如投资股票，如果看到某只股票突然猛涨或者猛跌就立马追涨杀跌，那么这样的策略大概率是很难稳定的获利的。所以PPO比之前的RL算法效果好的一个最本质的原因就是clip掉了那些有很大reward涨落的轨迹，让模型的优化更加稳定。
  • 所以从这个角度看，RL这个算法天然地就会限制LLM模型后训练之后和之前的差别（更像是分布的锐化，而非参数空间的巨大改变），所以遗忘现象没有普通的sft严重也是很合理的事情了。
• SFT和RL的loss 形式一致但训练差异性较大，说明我们应该聚焦在两种训练方式的数据分布究竟有何差异。
• 《The Entropy Mechanism》 关注的是宏观的、全局的“策略熵” (Policy Entropy)。它关心的是模型在RL训练过程中的整体健康状况，特别是策略熵是否会过早 “崩溃”。
• 《Beyond the 80/20 Rule》 关注的是微观的、局部的“Token级熵” (Token-level Entropy)。它把熵当作诊断工具，去寻找推理链条中那些最关键的“分叉路口”。
• RL训练的本质，是模型在“探索多样性”（高熵）和“追求正确答案”（高奖励）之间进行的一场极限拉扯。
• 为什么会发生“熵崩溃”？论文从数学上给出了一个解释。作者推导出，策略熵的变化与一个关键因素——动作概率和优势函数（Advantage）的协方差——有关（反比关系）：
  • 当模型选择一个高概率的动作（token），而这个动作又带来了高奖励（高Advantage）时，强化学习算法会大力强化这个选择。
  • 这种“强强联合”的更新，会导致这个高概率动作的概率变得更高，其他动作的概率被压制，从而使得整个概率分布的熵急剧下降。
• RL for Reasoning的有效性，几乎完全来自于对这20%高熵“关键少数”的优化。
• RL并不是在机械地加强一整条“正确答案”的路径。它真正的作用，是帮助模型学会在那些充满不确定性的关键决策点，如何做出更优的选择。那80%的低熵部分，模型在SFT阶段已经学得很好了，再用RL去“用力”，反而是浪费计算资源，甚至可能破坏模型的语言流畅性。

一、熵、交叉熵、KL散度

《The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models》
https://arxiv.org/abs/2505.22617
《Beyond the 80/20 Rule: High-Entropy Minority Tokens Drive Effective Reinforcement Learning for LLM Reasoning》
https://arxiv.org/abs/2506.01939

0、信息论之父香农（Shannon）的熵定义：对于一个离散变量 X ，其概率分布为 $P(x)$ ，那么它的信息熵 $H(P)$ 定义为：
$$H(P)=-\sum _{x}P(x){\log }_{2}P(x)$$

• $P(x)$ 是事件 $x$ 发生的概率。
• ${\log }_{2}P(x)$ 可以理解为事件 x 发生所包含的＂信息量＂或＂惊奇程度＂（概率越低，信息量越大）。
• 前面的负号是了确保熵值为正。
• 整个公式就是对所有可能事件的＂期望信息量＂或＂期望惊奇程度＂进行加权平均。

2、交叉熵：衡量的是，当我们用模型的＂有偏认知＂$(Q)$ 去预测和编码＂客观事实＂$(P)$ 时，所需要的平均信息量。它的公式是：
$$H(P,Q)=-\sum _{x}P(x){\log }_{2}Q(x)$$

注意：交叉熵只是 $\log$ 里的概率从 $P(x)$ 换成了 $Q(x)$ 。然而由于我们的模型Q总是不完美的，所以用它来编码 $P$ 的代价 $H(P,Q)$ ，必然会比用 $P$ 自己最优的编码代价 $H(P)$ 要高。多出来的这个代价就是KL散度（衡量两个概率分布的距离）。

3、交叉熵，信息熵和KL散度之间存在以下关系：

$$\text{ 交叉熵 }(H(P,Q))=\text{ 信息熵 }(H(P))+\mathrm{KL}\text{ 散度 }\left(D_{KL}(P\Vert Q)\right)$$

4、KL散度的计算方式：
$$D_{KL}(P\Vert Q)=H(P,Q)-H(P)=\sum _{x}P(x){\log }_2\frac{P(x)}{Q(x)}$$

注意：SFT微调时，我们接触到的真实数据（各种训练语料）是固定的，所以真实世界的信息熵 是一个我们无法改变的常数。因此，我们的优化目标就等价于最小化模型预测Q和真实数据P之间的KL散度。

5、SFT和RL的loss区别（token维度的观察）：
（1）SFT 的 loss 是目标分布和模型分布的交叉熵函数：给定目标分布 $q$（通常是 one－hot），模型预测分布 ${\pi }_{\theta }$ ，交叉熵定义为：

$${\ell }^{\mathrm{CE}}\left(q,{\pi }_{\theta }\right)=-\sum _{k}q(k)\log {\pi }_{\theta }(k)$$

在 SFT 中，我们有一个 参考答案 $a_t$ ，所以目标分布是：$q(k)=1\left[k=a_t\right]$

综上，SFT 的单个 token 的loss 是：

$${\ell }_t^{\mathrm{SFT}}(\theta )=-\sum _{k}1\left[k=a_t\right]\log {\pi }_{\theta }(k)=-\log {\pi }_{\theta }\left(a_t\right)$$

令 loss 对 logits 向量 $z$ 求导得：${\nabla }_{z_{t,k}}{\ell }_t^{\mathrm{SFT}}={\pi }_{\theta }(k)-1\left[k=a_t\right]$ （SFT单个token的loss梯度）

（2）强化学习REINFORCE 单个 step 的 loss 是 ${\ell }_t(\theta )=-A_t\cdot \log {\pi }_{\theta }\left(a_t\right)$

已知 transformer 的每个 step 的输出是一个 logits 向量，对这个 logits 做一次 softmax 函数就得到了每个 token 被选中的概率。如果记 $z$ 为 logits 向量，那么 $\pi =\mathrm{softmax}(z)$

令 loss 对 logits 向量 $z$ 求导得：${\nabla }_{z_{t,k}}{\ell }_t=A_t\cdot \left({\pi }_{\theta }(k)-1\left[k=a_t\right]\right)$ （RL单个token的loss梯度）

• 当 $k=a_t$（被选中的 token）$\pi (k)-1<0$ 所以如果 $A_t>0$ ，这个 logit 被推高
• 当 $k\ne a_t$（未选中的 token）$\pi (k)-0>0$ 所以如果 $A_t>0$ ，这个 logit 被推低

注意：

• $A_t(\pi )$是一个随着$\pi$变化而变化的优势估计函数，无法对该优势估计函数进行求导，只能通过采样来评估，采样必然存在误差，进而导致训练不稳定。
• 可见SFT和RL的loss形式是类似的， 但训练差异性较大，说明我们应该聚焦在两种训练方式的数据分布究竟有何差异。

二、微观的Token熵与宏观的策略熵

1、​​奖励的提升 ≈ 熵的消耗

​​奖励的提升 ≈ 熵的消耗

论文发现了一个经验公式：$R=-a\cdot e^H+b$ ，其中 $R$ 是奖励，$H$ 是熵。这个公式明确告诉我们：奖励的提升，是用熵的消耗换来的。当熵（探索能力）耗尽时，性能的提升也就到头了。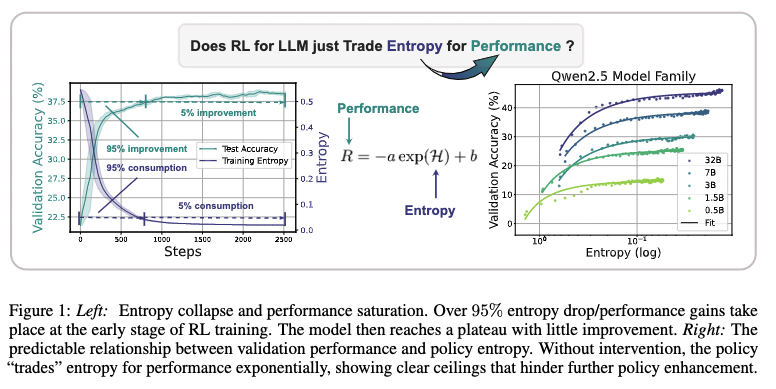

2、为啥会发生熵崩溃

为什么会发生“熵崩溃”？论文从数学上给出了一个解释。作者推导出，策略熵的变化与一个关键因素——动作概率和优势函数（Advantage）的协方差——有关（反比关系）。原文中的公式比较复杂，感兴趣的读者可以自行拜读。这里提供一个通俗易懂的说法（在数学上不一定严谨）。简单来说：

• 当模型选择一个高概率的动作（token），而这个动作又带来了高奖励（高Advantage）时，强化学习算法会大力强化这个选择。
• 这种“强强联合”的更新，会导致这个高概率动作的概率变得更高，其他动作的概率被压制，从而使得整个概率分布的熵急剧下降。

在RL训练初期，模型很容易找到一些“低垂的果实”，即一些简单、高回报的捷径。于是模型疯狂地在这些路径上进行自我强化，导致协方差持续为正，熵一路狂跌，最终“熵崩溃”，探索能力耗尽。

为了解决这个问题，论文提出了Clip-Cov和KL-Cov等方法，核心思想就是限制那些高协方差token的更新幅度。翻译成大白话就是：“我知道你这个选择又自信又正确，但你先别太激动，悠着点更新，给别的可能性留点机会。”

3、二八原则

《Beyond the 80/20 Rule: High-Entropy Minority Tokens Drive Effective Reinforcement Learning for LLM Reasoning》
https://arxiv.org/abs/2506.01939

RL训练真正起作用的，是优化那些“高熵”的关键决策点。​​
文章发现了一个“二八定律”：

• ​​80%的Token是低熵的​​：这些是推理过程中的“废话”或确定性的计算步骤（比如“因此”、“答案是”、“=”等）。模型生成这些词时很确定，RL训练对它们用力是白费功夫。
• ​​20%的Token是高熵的​​：这些才是真正的 ​​“思维分叉路口”​​ ！比如，在解一道数学题时，决定“是先求面积还是先求周长？”；在逻辑推理中，决定“这个证据是支持A观点还是B观点？”。在这些节点上，模型非常纠结，熵很高。

研究者做了对比实验：

• ​​正常RL训练​​：更新所有Token。
• ​​只更新高熵Token​​：只在那20%的关键决策点上进行RL训练。
• ​​只更新低熵Token​​：只在那80%的“废话”上进行RL训练。

结果令人震惊：

• ​​“只更新高熵Token”的效果，和“正常RL训练”差不多，有时甚至更好！​​
• ​​“只更新低熵Token”的效果一塌糊涂。​

实验结论：RL并不是在机械地加强一整条“正确答案”的路径。它真正的作用，是帮助模型学会在那些充满不确定性的关键决策点，如何做出更优的选择。那80%的低熵部分，模型在SFT阶段已经学得很好了，再用RL去“用力”，反而是浪费计算资源，甚至可能破坏模型的语言流畅性。

Reference

[1] https://zhuanlan.zhihu.com/p/1954330684970754139
[2] 《The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models》
[3]《Beyond the 80/20 Rule: High-Entropy Minority Tokens Drive Effective Reinforcement Learning for LLM Reasoning》
[4] 以信息熵的角度解构RL！大白话讲从“熵”到“RL”的探索之路
[5] RL 为什么不如 SFT 稳定？以及 RL 各种 Trick
[6] SFT和RL，在后训练中哪个更容易导致遗忘？